Basic network transformations

Network transformations are useful to adjust the transfer function or to optimize the network properties. The command

transform: lowpass( <bandwidth> );

will scale the bandwidth of the filter with a factor <bandwidth>. This is useful to modify the bandwidths of the filters that FA generates to realize one of the standard transfer functions of Section 5.

The command

transform: bandpass( <ω₀ >, <ω_c >);

transforms a lowpass filter into a bandpass filter. This will double the order of the filter. The bandwidth of the resulting filter is ω_c times the bandwidth of the original lowpass filter. The central frequency of the bandpass filter is ω₀ .

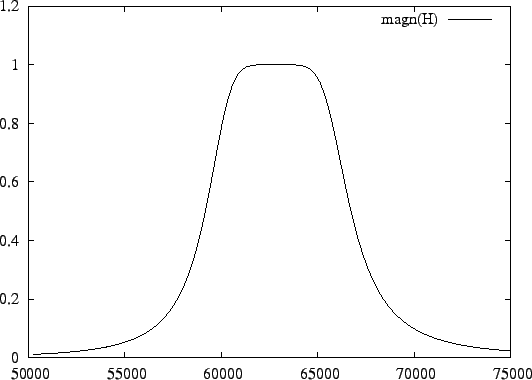
With the following input

butterworth(3);
transform: bandpass( 2 * pi * 1e4, 2 * pi * 1e3);
output: filter;
freq=lin( 2 * pi * 0.8e4, 2 * pi * 1.2e4, 100);
plot: magn(H);

the initial lowpass equivalent filter is transformed to a bandpass filter with a central frequency of 10kHz and a bandwidth of 1kHz, the state-space representation of which is in the output file:

(6, 6)
  -6.283185e+03   6.283185e+04   6.283185e+03   0.000000e+00   0.000000e+00   0.000000e+00
  -6.283185e+04   0.000000e+00   0.000000e+00   0.000000e+00   0.000000e+00   0.000000e+00
  -3.141593e+03   0.000000e+00   0.000000e+00   6.283185e+04   3.141593e+03   0.000000e+00
   0.000000e+00   0.000000e+00  -6.283185e+04   0.000000e+00   0.000000e+00   0.000000e+00
   0.000000e+00   0.000000e+00  -6.283185e+03   0.000000e+00  -6.283185e+03   6.283185e+04
   0.000000e+00   0.000000e+00   0.000000e+00   0.000000e+00  -6.283185e+04   0.000000e+00

B =
(6, 1)
   1.256637e+04
   0.000000e+00
   0.000000e+00
   0.000000e+00
   0.000000e+00
   0.000000e+00

C =
(1, 6)
   0.000000e+00   0.000000e+00   0.000000e+00   0.000000e+00   1.000000e+00   0.000000e+00

D = 0.000000e+00

The magnitude plot is shown in Figure 8.

Figure 8: The magnitude response of a filter after transformation to a bandpass filter.

It is usually a good idea to perform network analysis and manipulation before lowpass and bandpass transformation. Operations are usually numerically better conditioned on a unity-bandwidth prototype than on a filter with a very large or small bandwidth. This is especially the case for bandpass filters because they have twice the order. Many operations remain valid after transformation. For instance, dynamic range and scaling conditions remain unchanged after lowpass transformation.